Синтез и исследование логических схем
Задачи для самостоятельного исследования Задача].
Разработать логические схемы для реализации частично определенных логических функции F 4-х аргументов, заданных таблицами. Каждая комбинация значений аргументов двоичных переменных ABCD отображается числом N, равным: 23D + 22C + 2'В + 2°А. Значения функций при неуказанных комбинациях значений аргументов необходимо доопределить для получения схемы с минимальным числом элементов. Минимизацию логической функции проводить с помощью карт Карно или при помощи логического преобразователя.
Разработку провести на базе следующих типов элементов и схем:
• Элементы 2И, 2ИЛИ, НЕ;
• Элементы 2И-НЕ;
• Элементы 2ИЛИ-НЕ;
• Логические схемы серии 74, содержащие указанные элементы.
Пример: таблица 12.15 соответствует таблице 12.14. Таблица 12.14
N
4
6
7
8
9
11
12
13
14
15
Р
0
1
1
0
1
1
0
0
0
1
Таблица 12.15
N
D
C
B
А
F
4
0
1
0
0
0
6
0
1
1
0
1
7
0
1
1
1
1
8
1
0
0
0
0
9
1
0
0
1
1
11
1
0
1
1
1
12
1
1
0
0
0
13
1
1
0
1
0
14
1
1
1
0
0
15
1
1
1
1
1
Из карты Карно, составленной при помощи таблицы 12.15, следует, что минимальный вариант решения задачи имеет вид:
Варианты таблиц к задаче 1:
1
N
1
2
3
4
6
7
8
9
11
12
F
0
0
1
0
1
1
0
1
1
0
2
N
0
2
3
5
6
7
8
9
13
15
F
0
1
0
0
1
1
0
0
1
0
3
N
1
2
3
4
6
7
9
12
13
14
F
0
1
1
0
1
0
0
1
0
1
4
N
0
2
3
5
6
7
8
10
12
13
F
0
1
1
0
0
1
1
1
0
0
5
N
0
1
3
4
6
9
10
11
14
15
F
0
1
0
0
0
1
0
1
1
1
6
N
0
1
2
5
7
10
11
13
14
15
F
0
0
0
1
0
1
0
1
1
1
7
N
1
3
4
5
6
10
11
12
14
15
F
0
0
1
0
0
1
1
1
1
0
8
N
0
2
4
5
6
8
10
11
14
15
F
1
0
0
0
0
1
1
1
0
1
9
N
0
1
3
4
5
6
9
10
11
14
F
0
1
0
1
1
0
1
0
1
0
10
N
0
1
2
4
5
7
10
11
13
15
F
1
0
0
1
1
0
0
0
1
1
Задача 9.
Вызовите генератор слов и логический анализатор. Запрограммируйте генератор на формирование последовательности четырехразрядных слов, соответствующих числам натурального ряда от 0 до 15. Подключите его выходы к соответствующим входам схемы, приведенной на рисунке (А - младший разряд числа, D - старший). Исследуйте работу схемы в режимах "STEP" и "CYCLE".
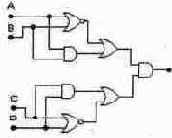
Нарисуйте временные диаграммы сигналов на выходах всех логических элементов схемы для всех возможных комбинаций входных сигналов. Проверьте правильность выполнения задания с помощью логического анализатора. Задача 10.
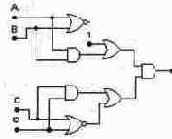
Проведите анализ работы схемы, изображенной на рисунке, для чего составьте таблицы реализуемых функций, если сигнал в точке 1 воспринимается элементом ИЛИ а) как логическая 1, б) как логический 0. Выберите необходимые инструменты для проведения экспериментальной проверки схемы и определите, как воспринимается сигнал на неподключенном входе при работе базовых элементов.
Задача 11.
Определите, как изменится работа схемы, приведенной в задаче 8, если произошел обрыв во входной цепи одного из элементов И, как показано на рисунке. Изменится ли характер восприятия сигнала на оборванном входе при замене логического элемента И на ИЛИ?
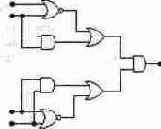
Задача 12.
Проведите анализ работы логического устройства, собранного на микросхемах 7404 и 7410, показанного на рисунке. Определите, какую математическую операцию выполняет данное устройство, если комбинации логических уровней на входе рассматривать как числа. Соберите схему, подключите необходимые приборы и проведите экспериментальное исследование работы схемы.
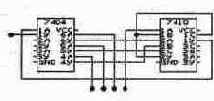
Задача 13.
Составьте логическое выражение, описывающее работу схемы, приведенной на рисунке. Определите, какую математическую операцию выполняет данная схема. Преобразуйте схему таким образом, чтобы получить устройство для выполнения той же операции над двумя 4-разрядными числами.
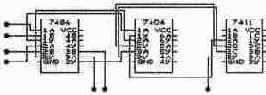
Задача 14.
Разработайте схему устройства, которое формирует на выходе сигнал, равный 1 при выполнении условия N1>N2, где N1 и N2 - трехразрядные числа, определяемые комбинациями логических уровней на входах схемы. Выполните задание: а) на элементах И, ИЛИ и НЕ; б) на элементах ИСКЛЮЧАЮЩЕЕ ИЛИ, И, НЕ. Укажите, какая элементная база позволяет получить более простые схемотехнические решения устройств сравнения. Задача 15.
Разработайте схему, формирующую на выходе сигнал F из входных сигналов А, В, С, как показано на рисунке.
Соберите схему. При проверке ее работы для формирования входных сигналов используйте: а) источники логических сигналов, б) генератор слов. Задача 16.
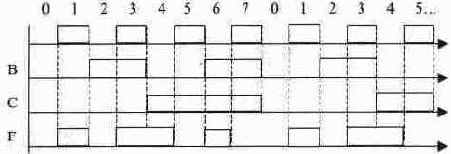
Разработайте схему, содержащую минимально возможное число базовых элементов, работа которой описывается временными диаграммами на рисунке (А, В, С - входы, F - выход схемы).
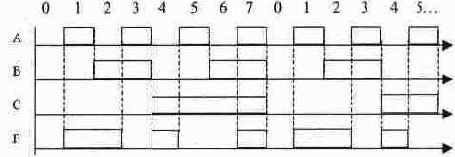
Задача 17.
Произведите изменения в приведенной на рисунке схеме, необходимые для того, чтобы она реализовала ту же функцию, что и в задаче 16. Указание: Минимальные изменения требуют введения элемента НЕ в разрыв одной из цепей.
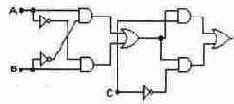
Задача 18.
Как можно упростить схему предыдущей задачи, чтобы выполняемая схемой функция не изменилась? Задача 19.
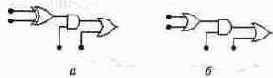
При монтаже схемы, приведенной на Рис. а, была допущена ошибка: вместо элемента исключающее ИЛИ был использован элемент ИЛИ (Рис. б). Найдите комбинации входных сигналов, которые позволяют выявить ошибку монтажника.