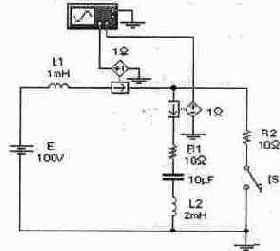
с двумя реактивными элементами рассмотрим
Упражнения
8.2. Анализ процессов в сложных схемах
Методические указания Методику расчета и экспериментального исследования процессов в сложных цепях с двумя реактивными элементами рассмотрим на конкретном примере, проведя расчет классическим и операторным методами и сравнив результаты расчета и эксперимента. Задача 1. Переходный процесс при мгновенном изменении параметров цепи.
Рассчитать напряжение на конденсаторе Uc(t) и ток ic(t) в катушке в схеме, приведенной на рис. 8.6 (файл с8_06) при закорачивании ключом [Space] сопротивления R2. При расчете принять, что переключение происходит из установившегося режима.
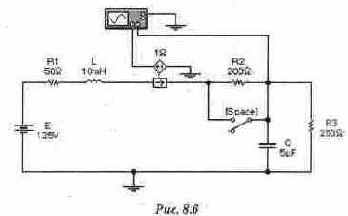
Расчет классическим методом Шаг 1. Нахождение корней характеристического уравнения. Характеристическое уравнение имеет вид:

Шаг 2. Определение констант в уравнении для тока через катушку. Поскольку корни характеристического уравнения комплексно-сопряженные, переходной процесс носит колебательный характер и, следовательно, ток через индуктивность iL(t) выражается следующей зависимостью:
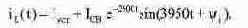
Уравнение (8.10) содержит две константы, для определения которых необходимо решить систему двух уравнений, одним из которых является само уравнение (8.10). Вторым уравнением, содержащим те же константы, является уравнение для производной тока через индуктивность:
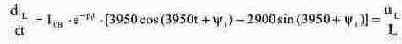
Для определения указанных констант при классическом методе расчета используются уравнения (8.10) и (8.11). Рассмотрим порядок вычисления значений этих выражений в момент t = 0+. Закон коммутации для катушки индуктивности формулируется в следующем виде: iL(0+)=iL(0-). (8.12) Подставляя t=0 в уравнение (8.10), получим уравнение, описывающее состояние схемы до коммутации:
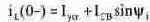
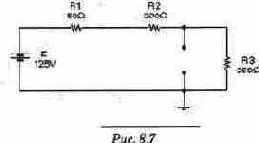
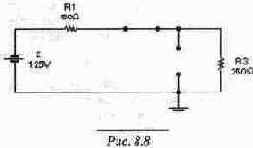
Значение iL(0-) является установившимся значением тока при разомкнутом ключе. Схему замещения для определения этого тока получим, заменив катушку индуктивности в исходной схеме проводником, а конденсатор - разрывом (рис. 8.7). Из этой схемы находим ток до момента коммутации: iL(0-)= 125 В/500 Ом = 0.25 А. Ток Iуст является установившимся значением тока при замкнутом ключе. Схему замещения для определения этого тока получим, исключив из схемы рис. 8.7 сопротивление R2, закороченное ключом (рис. 8.8). Из схемы находим ток в установившемся режиме после коммутации: Iуст= 125 В / 300 Ом = 0.417 А. Подставляя вычисленные значения iL(0-) и Iуст в (8.13), получим первое уравнение для вычисления констант: IcвSinфi =-0.167. (8.14) Рассмотрим теперь уравнение для производной тока в момент времени t(0+). Подставив t= 0 в уравнение (8.11), получим следующее выражение:
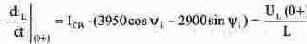
где правая часть получена из компонентного уравнения:
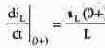
Значение UL(0+) не регламентируется непосредственно законами коммутации и для его вычисления нужно использовать оба закона коммутации наряду со вторым законом Кирхгофа. Рассмотрим, как изменяются напряжения на отдельных компонентах
схемы при коммутации. Напряжение на идеальном источнике питания не зависит от состояния схемы; напряжение на сопротивлении R1 измениться не может, поскольку не изменяется ток через индуктивность; напряжение на конденсаторе С также не может измениться по закону коммутации. В то же время напряжение на ключе, равное в момент времени t(0—) напряжению на сопротивлении R2, падает после коммутации до 0. Чтобы второй закон Кирхгофа выполнялся для момента t=(0+), это напряжение должно появиться на катушке индуктивности. Подставляя значение этого напряжения в (8.15), получим второе уравнение для вычисления констант:
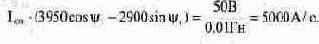
Далее решаем систему из двух уравнений (8.14) и (8.16). Из уравнения (8.14) получим:

Подставив это выражение в (8.16), определим:
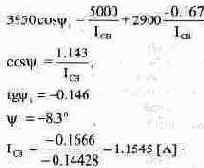
Ток через катушку индуктивности после подстановки констант в (8.10) вычисляется из выражения:
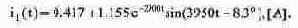
Шаг 3. Определение констант в уравнении для напряжения на конденсаторе. Результат получим, действуя аналогично изложенному в шаге 2: Напряжение на конденсаторе при колебательном переходном процессе выражается зави симостью:
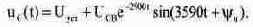
Уравнение для производной напряжения на конденсаторе:
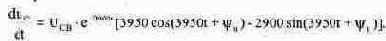
Согласно закону коммутации:
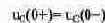
Величина Uc(0+) является установившимся значением напряжения на конденсаторе при разомкнутом ключе. Его можно рассчитать из схемы замещения, представленной на рис. 8.7. Uc(0-)= 125-250/500 = 62.5 В.
Напряжение UycT является установившимся значением напряжения на конденсаторе при замкнутом ключе. Его также можно получить из схемы замещения, представленной на рис. 8.8. Из схемы получим:
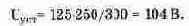
Подставляя вычисленные значения в (8.18), получим для момента t = 0:
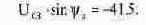
Производную напряжения для момента t(0+) можно вычислить подставив в (8.19) значение t = 0:
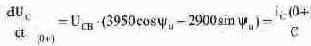
где правая часть получена из компонентного уравнения:
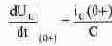
Значение ic(0+) не регламентируется непосредственно законами коммутации и для его вычисления нужно использовать оба закона коммутации наряду с первым законом Кирхгофа. Рассмотрим, как изменяются токи в ветвях, подходящих к узлу 1 на рис. 8.6 при коммутации. По закону коммутации ток через катушку не может измениться; по другому закону коммутации не может измениться и напряжение на конденсаторе (равное напряжению на резисторе Rз), и, соответственно, ток через Rз. Поэтому неизменным остается и ток через конденсатор, который до переключения ключа в установившемся режиме был равен нулю. Подставляя значение этого тока в уравнение (8.22) получаем:
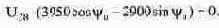
Из уравнения (8.21) получим:
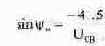
Теперь из уравнения (8.23) можно непосредственно вычислить угол, а затем и Ucв-
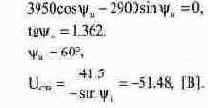
Напряжение на конденсаторе после подстановки констант вычисляется из выражения:
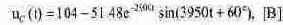
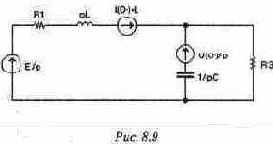
Расчет операторным методом Шаг 1. Составление операторной схемы замещения. При составлении операторной схемы замещения (рис. 8.9) элементы замещаются их операторными изображениями: индуктивность заменяется сопротивлением pL и источником ЭДС с напряжением L-iL/O-), отображающим наличие начального тока в катушке, емкость - сопротивлением 1/рс и источником ЭДС с напряжением Uc(0-)/p, отображающим начальное напряжение на конденсаторе, источник постоянной ЭДС - изображением Е/р, изображение резистора при переходе к операторной схеме совпадает с оригиналом. Начальные условия определяются так же, как и при расчете классическим методом, начальные значения тока через индуктивность и напряжения на емкости равны соответственно:
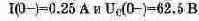
Шаг 2. Определение изображения тока в индуктивности. Найдем изображение тока методом эквивалентного генератора. Замещая эквивалентным генератором схему без левой ветви, найдем:
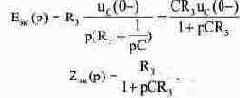
С учетом параметров эквивалентного генератора изображение тока в левой ветви:
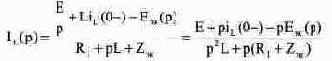
Подставляя значения Uэк(p) и Zэк(p). получим:
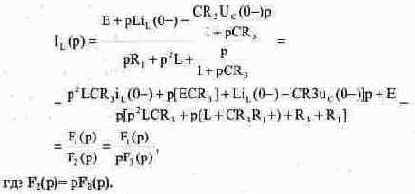
Подставляя значения параметров в Fl(p) и F2(p), получим:
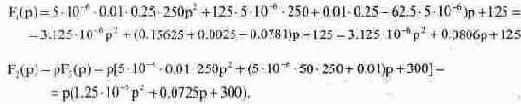
Шаг 3. Определение оригинала iL(t) по теореме разложения. В соответствии с теоремой разложения при колебательном характере процесса
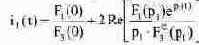
Подставляя в формулу (8.25) вычисленные выше значения F1(p) и F3(p) и производя преобразования, получим:
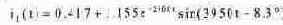
Корни характеристического уравнения F3(p)=0:
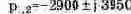
Вычисляем производную Fз'(p):
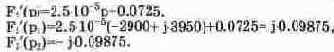
Определим F1(p1):

и, подставив полученное значение в (8.25), определим iL(t):
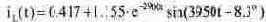
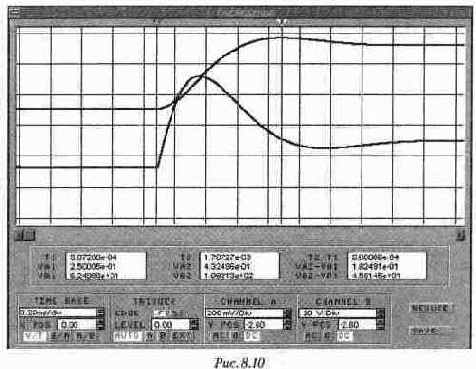
Аналогично можно определить и величину Uc(t). Экспериментальная проверка Для экспериментального определения величин Uc(t) и iL(t) можно воспользоваться увеличенной моделью осциллографа (рис. 8.10). Установив первый курсор в начале переходного процесса, а второй курсор на отметке текущего времени (800 мкс на рис. 8.10). С табло при этом считываем значения, соответствующие этому моменту времени (см. табл. 8.1). Таблица 8.1. Сравнение результатов расчета и эксперимента
t, мксек
Задачи для самостоятельного решения Задачи с 1 по 6 и с 24 по 26 приведены в книге, остальные задачи (с 7 по 23) вы сможете найти на прилагающихся к книге дискетах. 1. Схемы с конденсатором и катушкой индуктивности
Задача 1 (с8_11) Рассчитайте временные зависимости напряжения на конденсаторе С и тока через катушку индуктивности L при замыкании ключа [Space] и нулевых начальных условиях. Постройте графики соответствующих временных зависимостей. Результаты расчета проверьте с помощью Electronics Workbench.
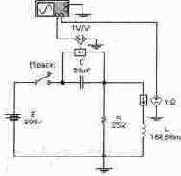
Задача 2 (с8_12) Рассчитайте временные зависимости напряжения на сопротивлении R и тока через катушку индуктивности L при замыкании ключа [Space] и нулевых начальных условиях. Постройте графики соответствующих временных зависимостей. Результаты расчета проверьте с помощью Electronics Workbench.
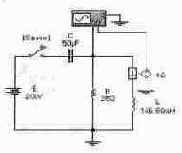
Задача 3 (с8_13) Рассчитайте временные зависимости напряжения на конденсаторе С и тока через катушку индуктивности L при размыкании ключа [Space] и постройте графики соответствующих временных зависимостей. Результаты расчета проверьте с помощью Electronics Workbench.
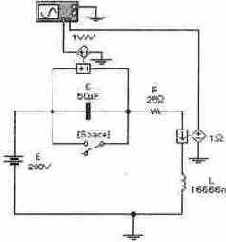
Задача 4 (с8_14) Рассчитайте временные зависимости напряжения на конденсаторе С и тока через катушку индуктивности L при замыкании ключа [Space] и нулевых начальных условиях. Постройте графики соответствующих временных зависимостей. Результаты расчета проверьте с помощью Electronics Workbench.
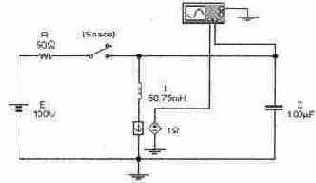
Задача 5 (с8_15) Рассчитайте временные зависимости напряжения на конденсаторе С и тока через катушку индуктивности L при замыкании ключа [Space] и нулевых начальных условиях. Постройте графики соответствующих временных зависимостей. Результаты расчета проверьте с помощью Electronics Workbench.
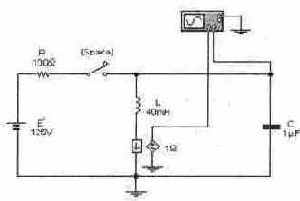
Задача 6 (с8_16) Рассчитайте временные зависимости напряжения на конденсаторе С и тока через катушку индуктивности L при замыкании ключа [Space] и нулевых начальных условиях. Постройте графики соответствующих временных зависимостей. Результаты расчета проверьте с помощью Electronics Workbench.
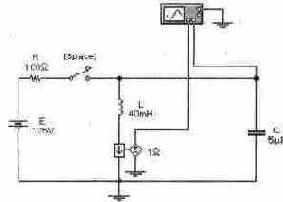
2. Переходные процессы при некорректных включениях
Задача 24 (с8_34) Рассчитайте временные зависимости напряжения на обоих конденсаторах и тока через резистор R при замыкании ключа [Space]. Постройте графики соответствующих временных зависимостей. Результаты расчета проверьте с помощью Electronics Workbench.
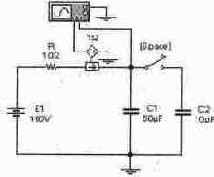
Задача 25 (с8_35) Рассчитайте временные зависимости токов через катушки индуктивности L1 и L2 при размыкании ключа [Space]. Постройте графики соответствующих временных зависимостей. Результаты расчета проверьте с помощью Electronics Workbench.
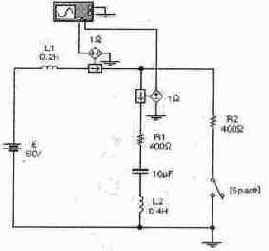
Задача 26 (с8_36) Рассчитайте временные зависимости токов через катушки индуктивности L1 и L2 при размыкании ключа [Space]. Постройте графики соответствующих временных зависимостей. Результаты расчета проверьте с помощью Electronics Workbench.