Частотные характеристики цепей без потерь
Методические указания Методику решения задач данного типа рассмотрим на конкретном примере Задача. Цепь без потерь
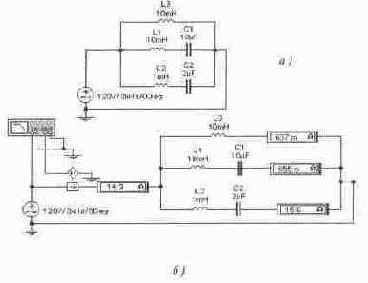
В схеме рис. 5.16 найти резонансные частоты и объяснить физическую природу и тип резонанса при каждой частоте. Провести экспериментальную проверку полученных частот с помощью Electronics Workbench. Измерить напряжения на каждом из параллельных резонансных контуров и входное напряжение при частотах до первого, между первым и вторым, между вторым и третьим и после третьего резонанса.
Экспериментальное исследование и анализ его результатов
Частотную характеристику (зависимость комплексного входного сопротивления от частоты) для рис. 5.16 можно получить из выражения
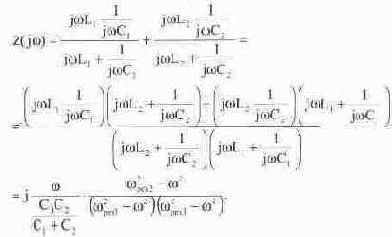
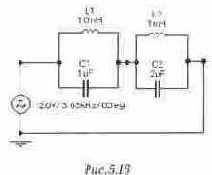
Для любого двухполюсника без потерь можно получить подобное уравнение комплексного входного сопротивления. При этом частоты, соответствующие резонансам напряжений (как частота (wрез2 в нашем случае), входят в числитель и образуют нули функции, а частоты, соответствующие резонансам тока (как wрез1 и wрез), входят в знаменатель и образуют полюса. Исследование частотных характеристик проведем в схеме рис. 5.17. Для того чтобы получить входное комплексное сопротивление, необходимо выход Боде-плоттера подключить к источнику питания, а вход — к датчику тока, в качестве которого используется
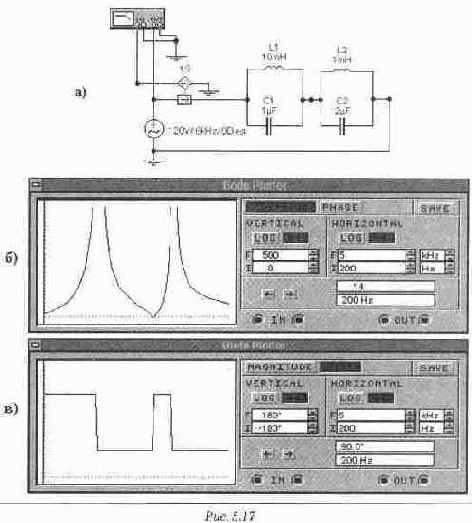
зависимый источник напряжения, управляемый током (см. методику измерения мгновенных значений тока). В этом случае отношение напряжений равно модулю входного сопротивления, а фазовый сдвиг напряжений определяет фазу входного сопротивления. Рассмотрим результаты экспериментальных исследований частотных характеристик (рис. 5.17). При нулевой частоте, то есть при постоянном токе, катушки индуктивности представляют собой короткое замыкание, конденсаторы — разрыв, поэтому при стремлении частоты к нулю почти весь ток проходит через катушки индуктивности, и проводимость контура носит индуктивный характер, что при отсутствии потерь обеспечивает угол ф=90". При повышении частоты сопротивление контура нарастает, как показывает ам-плитудно-частотная характеристика на рис. 5.176, и характер входного сопротивления остается индуктивным до частоты первого резонанса.
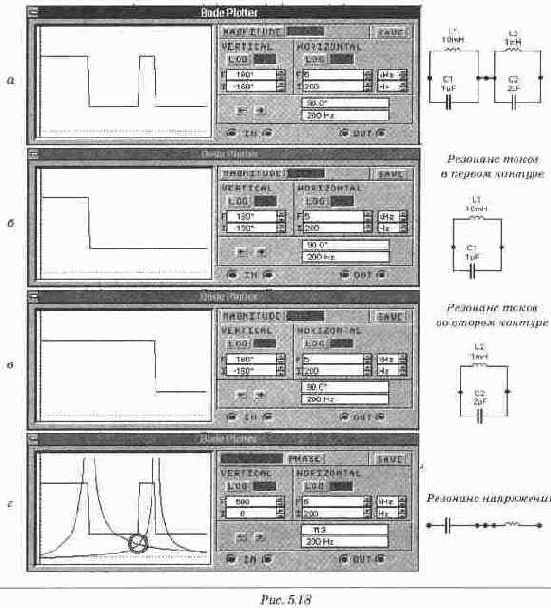
При частоте Fрeз1 (первая частота, при которой происходит изменение фазы входного сопротивления схемы на 180°) наступает резонанс в контуре Lq - Ci, у которого резонансная частота меньше (поскольку больше и индуктивность и емкость). Эта резонансная частота рассчитывается так же, как в простом LC-контуре и составляет

Это резонанс токов, и на рис. 5. 176 виден резкий рост сопротивления, поскольку при резонансе токов контур L2 - С2 можно рассматривать как разрыв цепи. При частоте, несколько большей Fpeз1, изменяется характер входного сопротивления, поскольку теперь проводимость конденсатора C1 больше проводимости катушки L1, и угол скачком изменяет свое значение от 90°до -90°. Ha рuc. 5.17в, однако, мы наблюдаем резкий переход, но не с бесконечно большой крутизной. Это объясняется тем, что при численных методах расчета, на которых основано моделирование в Electronics Workbench, принципиально не может быть бесконечно больших величин, в том числе и бесконечно больших производных по частоте. Следовательно, исследуя идеальные модели, какой является цепь без потерь, мы должны исключить из фазочастотной характеристики все точки, в которых углы отличаются от 90° или -90 и интерполировать характеристики с обеих сторон от частоты резонанса. При дальнейшем повышении частоты сопротивление контура L1 - C1, имея емкостной характер, начинает уменьшаться, в то время как сопротивление контура L2 - С2 сохраняет индуктивный характер и продолжает увеличиваться. При некоторой частоте Fpeз2 (второе изменение фазы входного сопротивления на 180°) модули этих сопротивлений сравниваются, и общее сопротивление цепи становится равным нулю, что характеризует резонанс напряжений. При дальнейшем росте частоты индуктивное сопротивление контура La - Са превосходит емкостное сопротивление контура L1 - C1, общий характер цепи становится индуктивным и угол скачком изменяет свое значение от -90°до 90° (рис. 5.17в). Рост модуля сопротивления продолжается до частоты резонанса токов в контуре L1 - C1, которая рассчитывается по формуле
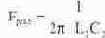
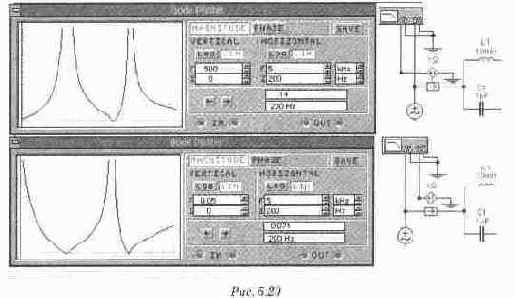
При дальнейшем росте частоты характер сопротивления в обоих контурах L1 - C1 и L2 - С2 становится емкостным и убывает по мере роста частоты. Наш качественный анализ позволил, тем не менее, вычислить две резонансные частоты Fpез1 и Ррез3. Подтвердить его правильность экспериментально можно, сравнивая фазочастотные характеристики (ФЧХ) для нашей схемы с ФЧХ для двух параллельных контуров L1 - C1 и L2 - С2 (рис 5.18). Как видно из рис. 5.18, частота первого резонанса токов совпадает с частотой резонанса для контура L1 - C1, частота второго резонанса токов с частотой резонанса для контура L2 — С2. Частоту резонанса напряжений можно определить из амплитудно-частотных характеристик двух контуров L1 - C1 и L2 — С2. Для определения построим на одном рисунке (рис. 5. 18в) фазочастотную характеристику общей цепи и амплитуд -но-частотные характеристики контуров L1 - C1 и L2 - C2. Это нетрудно сделать, используя программу Paint из стандартных программ Microsoft Office. Для этого нужно получить копию экрана с Боде-плоттером после анализа фазочастотной характеристики общей схемы, нажав клавишу Print Screen, вставить ее в файл
Paint и из общей картинки вырезать Боде-плоттер. Затем необходимо перенести его в другой файл через Clipboard. Затем из копии экрана, полученной после анализа амплитудно-частотной характеристики L1 - С1 контура, вырезать только экран Боде-плоттера и наложить на его на картинку Боде-плоттера в другом файле. Точно так же можно наложить и АЧХ L2 - С2 контура. Результат построения показан на рис. 5. 18г. Из него видно, что частота, при которой пересекаются нисходящая ветвь АЧХ L1 - С1 контура и восходящая ветвь АЧХ L2 - С2 контура (точка пересечения отмечена на рисунке кружком) совпадает с частотой резонанса напряжений, которую можно видеть из ФЧХ общей схемы. Из условия равенства модулей сопротивлений можно вычислить и частоту второго резонанса (резонанса напряжений между двумя контурами)
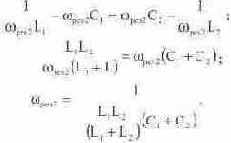
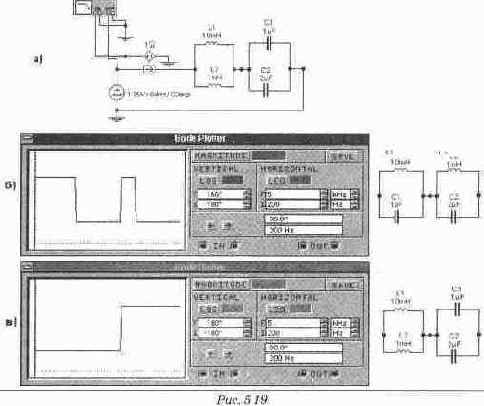
Из формального рассмотрения второго выражения можно сделать вывод, что частота этого резонанса должна совпадать с частотой резонанса в последовательном колебательном контуре, составленном из параллельно соединенных катушек L1 и L2 и параллельно соединенных конденсаторов С1 и С2 (рис. 5. 19а). Electronics Workbench позволяет получить этому наглядное экспериментальное подтверждение. Для этого необходимо сопоставить фазочастотные характеристики, снятые в исходной схеме (рис. 5. 196) и в схеме рис. 5. 19а (эта характеристика представлена на рис. 5. 19в).
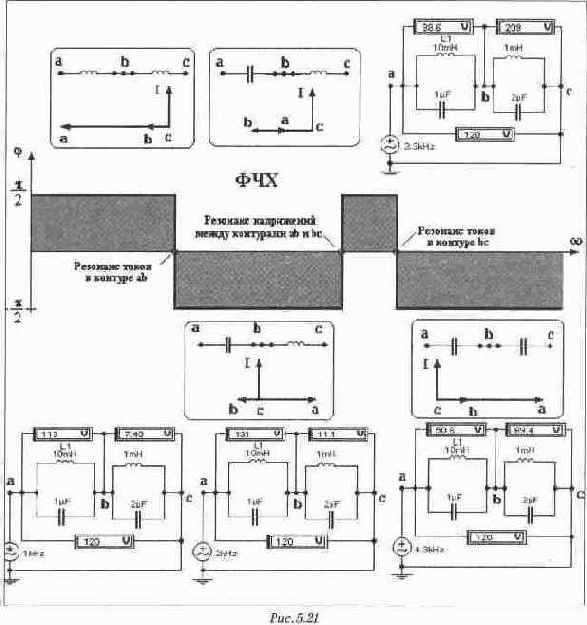
Отметим, что наиболее точное экспериментальное определение резонансной частоты из рис. 5. 17 удается осуществить для резонанса напряжении, поскольку нулевую точку характеристики легко определить. Для того, чтобы с такой же точностью определить частоты резонансов тока, целесообразно снимать вместо АЧХ входного сопротивления АЧХ входной проводимости исходной схемы. Для этого нужно только поменять местами вход и выход Боде-плоттера. На рис. 5. 20 представлены фрагменты схемы, позволяющие показать включение Боде-плоттера при снятии АЧХ сопротивления и проводимости и сами снятые АЧХ для исследуемой схемы. Рассмотрим, как изменяется векторная диаграмма для нашей схемы на различных частотных участках. Изменения в векторной диаграмме можно хорошо иллюстрировать и с помощью простых вольтметров (рис. 5. 21). На первом частотном интервале оба последовательных участка цепи имеют индуктивный характер (на рис. 5. 21 они замещены эквивалентными индуктивностями). Вследствие этого напряжение на каждом участке и общее напряжение, равное входному, опережают ток на 90°. Входное напряжение равно сумме напряжений на участках ab и bc. На втором частотном интервале (после резонанса токов в первом контуре) участок ab, как и вся схема, приобретает емкостной характер (на рис, 5. 21 он замещен эквивалентным конденсатором), характер участка bc остается индуктивным. На этом интервале входное напряжение равно разности напряжений на участках ab и bc, что видно и из векторной диаграммы. На третьем частотном интервале (после резонанса напряжений между двумя контурами) характер обоих участков ab и bc остается прежним, но индуктивное сопротивление участка ab преобладает, что приводит к изменению характера сопротивления всей схемы от емкостного к индуктивному. Входное напряжение также равно разности напряжений на участках ab и bc.
На четвертом частотном интервале (после резонанса токов во втором контуре) сопротивление второго контура становится емкостным. При этом эквивалентное сопротивление каждого из контуров носит емкостной характер и входное напряжение равно сумме напряжений на участках.
Задачи для самостоятельного исследования
Задача 13 (с5_23) Постройте и проверьте экспериментально зависимость входного сопротивления от частоты. Рассчитайте и определите экспериментально показания амперметров при резонансой частоте wреэ и частотах 0. 5 wрез и 2 (wрез-
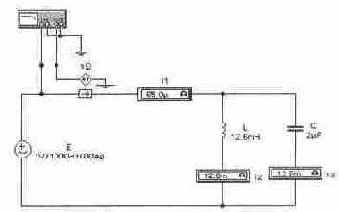
Задача 14 (с5_24) Нарисуйте (качественно) амплитудно-частотную и фазочастотную характеристики для входного сопротивления цепи. Рассчитайте резонансные частоты. Получите эти характеристики с помощью Боде-плоттера. Измерьте значения токов в LC-ветвях при частотах: F1 = 800 Гц, F2 = 2300 Гц и F3 = 7000 Гц. Объясните соотношение токов в ветвях при этих частотах.
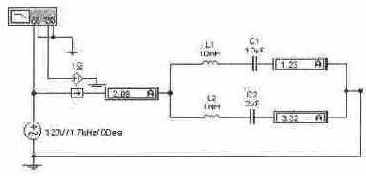
Задача 15 (с_25) Нарисуйте (качественно) амплитудно-частотную и фазочастотную характеристики для входного сопротивления цепи. Рассчитайте резонансные частоты. Получите эти характеристики с помощью Боде-плоттера. Измерьте значения напряжений на элементах цепи при частотах F1 = 100 Гц, F2 = 400 Гц и F3 = 1700 Гц и F4= 3200 Гц. Объясните соотношение напряжений при этих частотах.
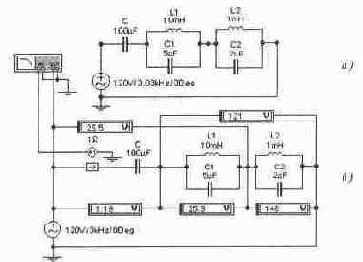
Задача 16 (с5_26) Нарисуйте (качественно) амплитудно-частотную и фазочастотную характеристики для входного сопротивления цепи. Рассчитайте резонансные частоты. Получите эти характеристики с помощью Боде-плоттера. Измерьте значения напряжений на элементах цепи при частотах F1= 300 Гц. F2= 1000 Гц, F3= 2500 Гц, F4= 15 кГц и F5= 50 кГц. Объясните соотношение напряжений при этих частотах.
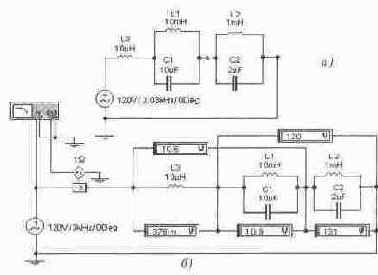
Задача 17 (с5_27) Нарисуйте (качественно) амплитудно-частотную и фазочастотную характеристики для входного сопротивления цепи. Рассчитайте резонансные частоты. Получите эти характеристики с помощью Боде-плоттера. Измерьте значения токов в LC-ветвях при частотах F1= 200 Гц, F2= 400 Гц, F3= 1 кГц, F4= 2. 5 кГц и F5= 3. 7 кГц. Объясните соотношение токов в ветвях при этих частотах.